0 9.10 2019 günü 15:30 da Kısacıkzade konağı Çukurova Üniversitesi Türkoloji Araştırmaları Merkezi Kültür evinde, Çağ Üniversitesi rektör Yardımcısı ve gazetemiz yazarı  Prof. Dr. Fikri
Akdeniz tarafından verilen altın oran konferansı ilgiyle izlendi.   Prof. Dr Deniz Abik’in daveti üzerine, Prof. Dr. Fikri Akdeniz tarafından gerçekleştirilen konferansta matematiksel güzellik, sayıların estetiğini ve doğada bir güzellik ölçütü olarak bilinen “altın oran” ve bu oranın 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,… biçimindeki Fibonacci sayıları ile ilişkisini dinleyicilerle paylaştı. “,618033989… sayısı ile ifade edilen altın oran ile doğada bitki ve canlılarda rastladığımız sarmal özellikleri anımsatarak Fibonacci sayılarını doğadan örneklerle tanıtan Prof. Dr Deniz Akdeniz; ayrıca, güzelliğin biyolojisini, bitkilerin algoritmik (bir ritim ve düzende) güzelliğini ve estetiğin matematiğini inceleyip;sanatta, mimaride, ve doğadaki bitki ve diğer canlılardaki altın oran uyumları konusundaki konferansını gerçekleştirdi.

*GÜZELLİK VE ALTIN ORAN

“Altın oran bir matematik kavramıdır. Fakat, uyum ve güzellik ölçütü olarak, sanat ve estetiğin bir sınıflandırmasıdır” diyen Prof. Dr. Fikri Akdeniz; “Güzellik, ölçülemeyen bir kavram
olmasına karşın güzellikle bağlantılı uyum,  formüllerle açıklanabilir. Güzellik: Sonuçta gözlerimize keyif veren, içimizde estetik bir his ve hayranlık oluşturan bir duygudur. Güzellik, bir canlının, somut bir nesnenin veya soyut bir kavramın algısal bir haz duyumsatan; hoşnutluk veren özelliğidir.  Güzellik, estetiğin, toplumbilimin, toplumsal psikolojinin ve kültürün bir parçası olarak incelenir”diyen Fikri Akdeniz; konuşmasını, “Altın oran insan tasarımından kaynaklanmadan doğada var olan biyolojik bir gerçektir. İnsan özellikle görsel yaratım alanında doğa’yı kültüre dönüştürmek istemiştir. Bu amaçla doğadan altın oranı almıştır. Altın orana, kısıtlayıcı değil de tam tersine çeşitlilikteki birliği yalınlaştıran bir etkiye yol açabilecek bir anlayışla bakılmalıdır.Altın oran, matematik ve sanatta, bir bütünün parçaları arasında gözlemlenen, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır” diyerek konuşmasını sürdürdü.
“İnsanoğlunun binlerce yıl boyunca süregelen doğayı anlama ve egemen olabilme çabalarının bir sonucu olarak ‘ne, neden, nasıl, ne zaman, kim, nerede?’ sorularının yanıtı aranmıştır. Bu çabaların sonunda elde edilen bilgiler, biçim, sayı ve çoklukların yapılarını, özelliklerini ve aralarındaki ilişkileri mantık yolu ile inceleyen ve sayı bilgisi, cebir ve geometri gibi dallara ayrılan bir bilimi yaratmıştır. Bu bilim dalı insanlığın ortak kültürünün çok önemli bir parçası olan matematiktir.” vurgusuyla konuşmasını dile getiren Akdeniz,matematik ne olduğu üzerine de şunları söyledi:  

O halde Matematik nedir?
“Emekli Eğitim Psikoloğu Prof. Dr. Eric De Corte (2004) tarafından “Yaşamın Soyutlanmış Bir Biçimidir." şeklinde yapılan tanım  en gerçekçi ve geniş haliyle matematiği ifade eder.  Matematik, zihinsel fonksiyonların gelişmesini sağlayan, yaşamı kolaylaştıran simgelerle ifade edilebilen kendine özgü bir dili olan bir bilim dalıdır. O halde matematik yaşam kadar eski, yaşamla birlikte gelişen, insanlık tarihi ile paralel bir gelişim gösteren bir bilim dalıdır. Matematiğin gelişimi ile bilimin ve uygarlıkların gelişimi arasında sıkı bir ilişki olduğunu biliyoruz. Macaristan doğumlu Matematikçi Paul Halmos’a (1916-2006) göre !Matematik bazı fikirleri daha kısa, daha yalın anlatabilmek için bulunmuş, her gün kullandığımız dilden daha kesin, daha ince bir dildir’ Bu yazımızda bu dili kullanarak bilim, doğa ve sanat arasındaki ilişkileri vereceğiz.

Altın oran doğada bir güzellik ölçütü olarak düşünüldüğüne göre doğaya anlamaya çalışmalıyız. Doğada kısa bir gezinti yaptığımızda doğadaki cisim ve canlılarla birlikte yaşadığımız halde onların sahip olduğu geometrik yapıyı, matematiksel özellikleri ve kusursuz simetriyi yakından izlediğimiz söylenebilir mi?

Ukrayna’lı düşünür Helena Blavatsky’nin (1831-1891) ifade biçimiyle: Doğa, içinde bir geometri olduğu için mi yoksa geometri doğanın her tarafında göründüğü için mi güzeldir? Bu güzellikleri görmek için kar taneciklerini incelemek, tavus kuşunun kuyruğunu kabartması durumunda çift yönlü oluşan sarmalları (spiralleri) seyretmek, papatyanın veya ayçiçeğinin ortasındaki iki yönlü sarmallara, çam kozalağına, arıların yaptıkları peteklerdeki geometrik yapıya, bazı bitki ve ağaç dallarındaki gelişime bakmak, dallar üzerindeki yaprakların dizilişini incelemek yeterli olacaktır. Doğa bu kadar güzel, uyumlu ve sır dolu olmasa (1170? -1250) yılları arasında yaşamış olan İtalya’lı matematikçi Fibonacci’nin adını O’nun adıyla anılan Fibonacci sayılarını belki de hiç duymazdık.”

*FİBONACCİ SAYILARI  
Fibonacci’nin 1170 yılında İtalya’nın Pisa kentinde doğduğunu, 1202 yılında tamamladığı “Liber Abaci” (Hesaplama Kitabı) adlı kitabında onluk sistemde nasıl aritmetik yapılacağını anlattığını ve yazdığı kitapta tavşan populasyonlarının çizelgesinin yapılmasıyla ilgili ilginç bir soru sorduğunu belirten Prof. Dr Deniz Akdeniz; orijinal problemin 1202 yılında Fibonacci tarafından ideal durumlarda tavşanların ne kadar hızlı yavruladıklarını göstermek amacıyla araştırıldığını söyledi. “Kabul edelim ki yeni doğmuş bir çift tavşanın biri erkek biri dişi olsun. Bunları belirlenmiş bir alana koyalım.” diyen Akdeniz; “Tavşanlar bir aylık olduklarında çiftleşebilecek duruma gelmektedirler. İkinci ayın sonunda dişi tavşanın diğer bir çift tavşan doğurduğunu kabul edelim. Tavşanlarımızın asla ölmediğini ve dişilerin ikinci aydan başlayarak her ay daima bir erkek bir dişi tavşan doğurduğunu kabul edelim.” dedikten sonra, Fibonacci’nin aşağıdaki soruyu sorduğunun altını çizdi…

“Bir yıl sonunda kaç çift tavşan olacaktır?,, Belirli bir alandaki tavşan çiftlerinin sayısı (1 çift ile başlandı)  1., 2., 3., 4., 5., 6., … ve izleyen aylar için 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,... olarak verilecektir. Bu sayı dizisine Fibonacci dizisi denir. Fibonacci dizisindeki ardışık iki sayının oranını alırsak, aşağıdaki kesirleri ve karşılık gelen ondalıklı sayıları buluruz.”

*Altın Dikdörtgen 

“Kısa kenarı 1 birim ve uzun kenarı altın orana, yani j=1,618.. ye eşit olan dikdörtgen düşünelim. Dikdörtgenin kenarları 1: oranına sahiptir. Böyle bir dikdörtgene ‘Altın dikdörtgen’ denir diyen Prof.Dr. Fikri Akdeniz; “aşağıdaki gibi üç kahverengi kutu ile gösterilen bir televizyon ekranı ya da bir yüzme havuzu tasarımı düşünüldüğünde göze en hoş görünen boyutlar ne olmalıdır? Bu sorunun yanıtı anket yapılarak öğrenilebilir. Uygulama sonucunda sağdaki altın dikdörtgen tüm dikdörtgenler içinde en estetik olarak önerilmiştir. Bu nedenle asırlardır sanat ve mimaride altın oran ve altın dikdörtgen geniş bir biçimde kullanılmıştır.” diyen Akdeniz;  Altı dikdörtgen için öncelikle günlük yaşamımızda kullandığımız kredi kartını ve oyun kartlarını verebiliriz. Ayrıca günümüzde bazı televizyon ve pullar üzerinde de altın dikdörtgen görülür.  
Aşağıdaki şekilde ardışık Fibonacci sayılarıyla (1,1,2,3,5,8,13,21,34,…)oluşturulan altın dikdörtgenler ve altın sarmalı göreceğiz.1 dedikten sonra altın sarmallar konusuna geçti

“Doğa’da Altın Sarmallar

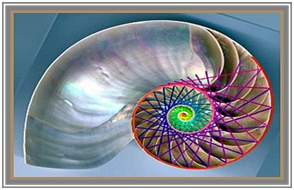
Sarmal’ın, merkezden sürekli uzaklaşan ve merkezi etrafında birçok defa dönen bir eğri olduğunu, sarmalın ilk kez Archimedes (M.Ö. 287?-212)  tarafından tanımlandığını; altın sarmalların, biyoloji dünyasında yaygın bir biçimde bulunduğunu; asma filizleri, sarmaşıklar, canlıların kalıtım molekülü DNA sarmal biçime uygun olduğunu anlatan Akdeniz; armak izleri, fillerin hortumları, bazı örümcek ağları, Evrendeki  galaksiler, nautilus, ayçiçeğinin kafasının bu tür sarmal için tipik örneklerdir. Ayçiçeğinde sarmalların sayıları 21/34, 34/55, 55/89 gibi ardışık Fibonacci sayıları olduğuna dikkat çekti.                                                                                   
“Nautilus: Deniz kabuklusu Nautilus’un iç kesiti ve kabuktaki sarmal eğriler görülmektedir. İçindeki odaları kullanarak hayvan bunları birbirine ekler ve gelişir. Kabuğun içindeki hayvan, sürekli kıvrılan bir boru oluştururken evini sürekli büyütür. Kabuk büyüdükçe, kabuğun içindeki hayvan da bir madde salgılayarak arkasında bir bölme yapar ve bu süreç devam eder. Altın oranla kontrol edilen bölmelerin gelişme modeli yukarıdaki nautilus kabuğunun kesitinde görülmektedir.” dedi.

Sanatta Altın Oran

Sanatta altın oran hakkında da konuşan Prof.Dr.Fikri Akdeniz, Gizemli güzelliğin, Leonardo da Vinci’nin (1452-1519) ünlü tablosu Mona Lisa’nın çizgilerinde ve tebessümünde gizli bir sırrı barındırdığı, tarih boyunca en çok tartışılan konulardan biri olduğuna değinirken;
Mona Lisa’nın yüzü etrafında bir dikdörtgen çizildiğinde, sonucun Altın dikdörtgen olduğunun görülebileceğini, ek olarak da, Mona Lisa tablosunda boyundan ellerin yukarısına kadar elbisenin yakasından ellerin altına kadar altın dikdörtgen biçimleri olduğunu, ayrıca resmin kendisinin de altın dikdörtgen içinde olduğunu söyledi.

Mona Lisa tablos
*El, Kol ve Parmaklarımızda Altın Oran

“Parmağımızdaki kemiklerin uzunluklarını ölçelim. 3 kemikten uzun olanının ortadakine bölümünden çıkan oran değeri nedir? Ayrıca ortadaki kemik uzunluğunun en küçük olanın uzunluğuna oranı hangi değeri vermektedir? Bulunacak değer yaklaşık olarak   olacaktır diyen Akdeniz; “dirsek-bilek uzunluğu ile el uzunluğunun oranından elde edilecek yaklaşık  değerlerini buluruz. Altın oranı kendi vücudumuzda da görebiliriz. İnsan vücudunun orantıları için altın oranın varlığı kanıtlanmıştır.”sözlerini dile getirdi.

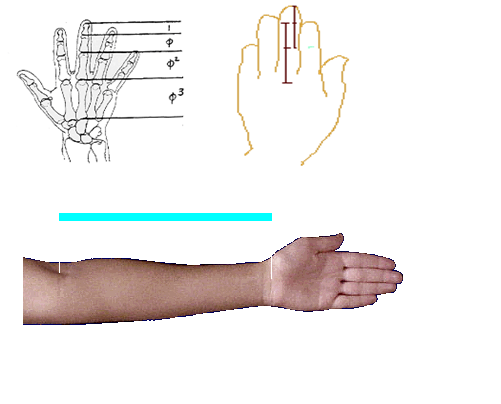
Parmaklardaki oranlar:

İnsan yüzünde de birçok altın oran olduğunu söyleyen Akdeniz; “Çünkü bu oranlandırma, bilim adamları ve sanatkârların birlikte kabul ettikleri ideal bir insan yüzü için geçerlidir. Her yüzün bu orana uyması beklenemez. Bu oranlar yalnız ideal yüzlerde bulunabilir.” Dedi.

Bitkilerde sarmallar ve altın oran

“Doğadaki çok şey Fibonaci sayı düzenini izlemektedir. Aşağıda bildiğimiz türden bir karnabahar resmi görülmektedir.  Dikkatli incelenirse en küçük çiçekçiğin merkez noktada olduğu görülür.  Çiçekçiklerin bu merkezin etrafında her iki yöne doğru sarmallar biçiminde düzenlendiği görülecektir.” diyen Akdeniz;  sözlerini, “Her iki yönde kaç sarmal vardır? Her bir yöndeki sarmalların sayısının Fibonacci sayı dizisinden olduğuna dikkat ediniz. Karnabaharın tabanına yakın bir küçük çiçekçiği koparıp daha yakından bakalım. Küçük karnabaharda da merkezin etrafında düzenlenmiş daha küçük çiçekçikleri görürüz. Sayma işlemi yapılırsa yine Fibonacci sayıları görülecektir. Circiumda 21/13 oranında sarmallar vardır.” açıklamasıyla sürdürdü. 

Karnabahar   
 Circium

Yaptığımız bu incelemenin sonunda çıkaracağımız sonuç nedir?

 “Altın oran, matematik ve fiziksel evrende daima varken, tam olarak, insan tarafından ne zaman bulunduğu ve uygulandığının bilinmediğine değenine Prof. Dr. Fikri Akdeniz konuşmasını şöyle sürdürdü:”Eski Yunan düşüncesine göre altın oran güzelliğin bir simgesiydi. Ayrıca, eski Yunanlılar güzelliğin üç bileşeninin olduğuna inanırlardı. Bunlar: simetri, orantı ve uyum (ahenk) dur. Günümüzde olduğu gibi antik çağda da “güzellik” ve “gerçek” arasında yakın bir matematiksel ilişki olduğunun farkına varılmıştı.

Bu yazı  ile estetiğin biyolojisini, doğadaki örüntü, güzellik ve uyumu; pozitif bilimlerle insan bilimlerini, Fibonacci sayılarını ve altın oranı kullanarak düşünmenize yardımcı olmak istedim. Bir buzdağının tepesini inceledik ve doğayı anlamaya çalıştık.” .